Question

use actuator-disk theory to show that the dynamic pressure in the ultimate wake of a propeller is equal to the sum of the free stream dynamic pressure and the disk loading (d. l.).

Answer 1

In actuator-disk theory, the dynamic pressure in the ultimate wake of a propeller is the sum of free stream dynamic pressure and disk loading, demonstrating a balance in aerodynamic forces.

Actuator-disk theory is a simplified aerodynamic model used to analyze the flow around a rotating disk, which can represent a propeller. In this theory, the flow is assumed to be axisymmetric, and the propeller is represented by a thin disk that imparts momentum to the air passing through it. The ultimate wake refers to the far downstream region where the effects of the propeller are fully developed.

Let's denote the following terms:

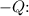`- \( Q \):` Dynamic pressure

-
`\( V_0 \)`: Free stream velocity

-
`\( r \)`: Radial coordinate measured from the center of the disk

-
`\( R \)`: Radius of the disk

-
`\( \rho \):` Air density

-
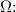`\( \Omega \):`Angular velocity of the disk (propeller)

The dynamic pressure at any point in the flow field is given by
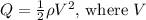`\( Q = (1)/(2) \rho V^2 \), where \( V \)` is the local velocity.

For actuator-disk theory, we consider the axial induction factor
`\( a \),`which represents the fraction of the free stream velocity
`\( V_0 \)` reduced by the presence of the disk. The local velocity \( V \) at any radial location \( r \) is then given by:

`\[ V = V_0 \cdot (1 - a) \]`

Now, the disk loading
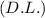`(\( D.L. \))` is defined as the thrust produced per unit span. It is related to the axial induction factor by the following expression:

`\[ D.L. = (1)/(2) \rho \cdot V_0 \cdot a \cdot (1 + a) \]`

Now, let's consider the ultimate wake, where the flow is fully developed. In this region, the local velocity
`\( V \)` becomes
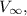`\( V_\infty \),` and the axial induction factor becomes
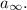`\( a_\infty \).` The dynamic pressure in the ultimate wake
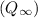`(\( Q_\infty \))` is then given by:

`\[ Q_\infty = (1)/(2) \rho \cdot V_\infty^2 \]`

Substituting the expression for
`\( V \) in terms of \( a \) into \( Q_\infty \),`we get:

`\[ Q_\infty = (1)/(2) \rho \cdot (V_0 \cdot (1 - a_\infty))^2 \]`

Now, we know that in the ultimate wake, the disk loading is equal to
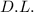`\( D.L. \)`. So, we can express
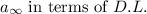`\( a_\infty \) in terms of \( D.L. \)` using the earlier expression for
`\( D.L. \).`

`\[ D.L. = (1)/(2) \rho \cdot V_0 \cdot a_\infty \cdot (1 + a_\infty) \]`