The dimensions for the surface area are
 m and
m and
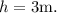
How did we get the value?
Assume that the length of a side of the rectangular base and top is (x) and the length of the vertical side is (h). The volume of the box is given by the product of the base area and the height. Now, equate this volume with the given volume of 27 cubic meters.
![\[ V = x^2 h \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/c3nr4af3wrzsu0evge1ri6wprrq05sjwag.png)
Given that the volume is 27 cubic meters:
![\[ x^2 h = 27 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/l8yinvwh68uw4i1uu55vqww9joaa6shnv6.png)
Express the surface area
 in terms of
in terms of
 and
and
 .
.
The surface area of the box is
![\[ A = 2x^2 + 4xh \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/bdplqmoqrcjvedjdm4bswepmymqzjnsuc9.png)
Substitute the expression for
 from the volume equation:
from the volume equation:
![\[ A = 2x^2 + 4x \left( (27)/(x^2) \right) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/g0ah2cna5l2xlq1mwb4qieg09kar4hcgkl.png)
![\[ A = 2x^2 + (108)/(x) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ura5pddfesxjpwpyhsvs4dup61owaed2al.png)
Take the derivative of
 with respect to
with respect to
 and set it equal to zero:
and set it equal to zero:
![\[ (dA)/(dx) = 4x - (108)/(x^2) \\= 0 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/8mo1rzyyr2byfoldckz83dk3361wyhq1j5.png)
Solving for
 :
:
![\[ 4x = (108)/(x^2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/w0egiyxc1ez9wet2uq85gcv5eqaus6smoa.png)
![\[ x^3 = 27 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/9366mdjyvjhssyul5h4hytzruxgwmihg18.png)
![\[ x = 3 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/etls0ppdon7wxc6tnfb3koevfbhpmmuheu.png)
Getting the value of
 , substitute it back into the volume equation to find
, substitute it back into the volume equation to find
 :
:
![\[ 3^2 h = 27 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/v3be5gv2hduuwd9zoutu37frw85dc7z9td.png)
![\[ 9h = 27 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/vqi6xgb56kopl29j6ewqkhsvms5s5p50m4.png)
![\[ h = 3 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/u2ne11a28go9gi8pheq87kd8n6zwdzhx9f.png)
So, the dimensions for the minimum surface area are
 and
and
