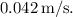Question

A student standing on a stationary skateboard tosses a textbook with a mass of mb = 1.5 kg to a friend standing in front of him. The student and the skateboard have a combined mass of mc = 105 kg and the book leaves his hand at a velocity of vb = 2.97 m/s at an angle of 26° with respect to the horizontal.

(a)Write an expression for the magnitude of the velocity of the student,vs, after throwing the book

Answer 1

The magnitude of the student's velocity after tossing the book is approximately
`\(0.042 \, \text{m/s}\)`, opposite to the book's velocity. This is determined by the conservation of linear momentum.

The law of conservation of linear momentum states that the total linear momentum of an isolated system remains constant if no external forces act on it. In this case, the student and the skateboard form an isolated system before and after the toss, so their total linear momentum remains constant.

The linear momentum before the toss is given by the combined mass of the student and skateboard,
`\(m_c\),` multiplied by their velocity,
`\(v_s\)`. The linear momentum after the toss is given by the sum of the linear momentum of the student and skateboard after the toss,
`\(m_c \cdot v_s\),` and the linear momentum of the book,
`\(m_b \cdot v_b\).`

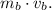
The equation representing the conservation of linear momentum is:

`\[ m_c \cdot v_{s,\text{before}} = m_c \cdot v_{s,\text{after}} + m_b \cdot v_b \]`

Before the toss, the student and skateboard are at rest (\(v_{s,\text{before}} = 0\)), so the equation simplifies to:

`\[ 0 = m_c \cdot v_{s,\text{after}} + m_b \cdot v_b \]`

Now, we can solve for the magnitude of the velocity of the student
`(\(v_s\))` after throwing the book.

`\[ m_c \cdot v_{s,\text{after}} = - m_b \cdot v_b \]`

`\[ v_{s,\text{after}} = - (m_b \cdot v_b)/(m_c) \]`

Now, substitute the given values:

`\[ v_{s,\text{after}} = - \frac{(1.5 \, \text{kg}) \cdot (2.97 \, \text{m/s})}{105 \, \text{kg}} \]`

`\[ v_{s,\text{after}} \approx -0.042 \, \text{m/s} \]`

The negative sign indicates that the student and skateboard move in the opposite direction to the book. Therefore, the magnitude of the velocity of the student after throwing the book is approximately
`\(0.042 \, \text{m/s}\).`