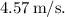The translational speed of the axle is approximately
To find the translational speed of the axle as the wheel rolls without slipping down an inclined plane, you can use the conservation of energy. The potential energy lost by the wheel as it descends the incline is converted into both translational kinetic energy and rotational kinetic energy.
The potential energy (PE) lost by the wheel is given by the equation:
![\[ PE = mgh \]](https://img.qammunity.org/2024/formulas/physics/high-school/hihu6zeucez3bf4r8udgxhwanpcnbf1dir.png)
where:
- \( m \) is the mass of the wheel,
- \( g \) is the acceleration due to gravity,
- \( h \) is the height of the inclined plane.
This potential energy is converted into translational kinetic energy
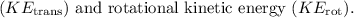
![\[ PE = KE_{\text{trans}} + KE_{\text{rot}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/z5a1f7zfo30f47h61vjiw2bthp8djwuai2.png)
The translational kinetic energy is given by:
![\[ KE_{\text{trans}} = (1)/(2)mv^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/neidrb3ooce566sf1iumzgrskfznkhr06o.png)
where \( v \) is the translational speed.
The rotational kinetic energy is given by:
![\[ KE_{\text{rot}} = (1)/(2)I\omega^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/on3x5mpawnzd2v025iyxq80iwaadqgm4e5.png)
where \( I \) is the moment of inertia about the axle and
 is the angular speed.
is the angular speed.
For a wheel rolling without slipping, the relationship between translational speed and angular speed is
 is the radius of the wheel.
is the radius of the wheel.
Now, let's set up the equations using the given information:
![\[ mgh = (1)/(2)mv^2 + (1)/(2)I\left((v)/(R)\right)^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/veazv81rmypvo5dpnww0b3u7jjqe9xtb9u.png)
Substitute \( I = mR^2 \) into the equation:
![\[ mgh = (1)/(2)mv^2 + (1)/(2)mR^2\left((v)/(R)\right)^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/kkv5kdxju4l6cnhbgy4rmvhoeie6lzmscp.png)
Simplify the equation:
![\[ mgh = (1)/(2)mv^2 + (1)/(2)mv^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/hne5yvebglpxjmoy5r80lbcwcm84dwbiwo.png)
Now solve for \( v \):
![\[ mgh = mv^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/9thp02s4yuuyme6rmg5emnzm6zradjya1g.png)
![\[ v = √(gh) \]](https://img.qammunity.org/2024/formulas/physics/high-school/on6g0z5cdxlmmpxpns1oa3fmwipk6sg43c.png)
Substitute the given values into the equation to find \( v \):
![\[ v = \sqrt{9.8 \, \text{m/s}^2 * 2.13 \, \text{m}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/hpp0pxxj7elr9c6b5rfjmkukrsknfslcho.png)
![\[ v \approx \sqrt{20.934 \, \text{m}^2/\text{s}^2} \]](https://img.qammunity.org/2024/formulas/physics/high-school/4orn0b8spant2t0hofpvhyam1lurl746mp.png)
![\[ v \approx 4.57 \, \text{m/s} \]](https://img.qammunity.org/2024/formulas/physics/high-school/t6y7r8csaj42k0hrbank0wvii0rc4off1o.png)
So, the translational speed of the axle is approximately