Question

On a level test track, a car with antilock brakes and 90% braking efficiency is determined to have a theoretical stopping distance (ignoring aerodynamic resistance) of 408 ft (after the brakes are applied) from 100 mi/h. The car is rear-wheel drive with a 110-inch wheelbase, weighs 3200 lb, and has a 50/50 weight distribution (front and back), a center of gravity that is 22 inches above the road surface, an engine that generates 300 ft-lb of torque, and overall gear reduction of 8.5 to 1 (in first gear), a wheel radius of 15 inches and a driveline efficiency of 95%. What is the maximum acceleration from the rest of this car on this test track

Answer 1

a = 30.832 ft/s²

Step-by-step explanation:

To solve this problem let's start by finding the braking acceleration using kinematics, where the distance is x = 408 ft, the initial velocity vo = 100 mi / h and the final velocity is zero v = 0

v² = v₀² - 2 a x

0 = v₀² - 2ax

a =
`(v_o^2)/(2x)`

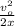
Let's start by reducing the magnitudes to ft / s

v₀ = 100 mi / h (5280 foot / 1 mile) (1h / 3600 s) = 146.666 ft / s

let's calculate

a =
`(146.66^2)/(2 \ 408)`

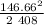
a = 26.36 ft / s²

Let's call this acceleration a_effective, this acceleration is in the opposite direction to the speed of the vehicle.

Let's use a rule of three (direct proportions) to find the acceleration applied by the brake system (a1) which has an efficiency of 95%. or 0.95

a₁ =
`(a_e)/(0.95)`

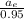
Let's use another direct proportion rule If the acceleration of the brake system (a₁) for an applied acceleration (a) with an efficiency of 0.90

a =
`(a_1)/(0.90)`

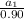
we substitute

a =
`(a_e)/(0.95 \ 0.90)`

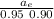
let's calculate

a =
`(26.36)/( 0.95 \ 0.90)`

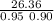
a = 30.832 ft/s²

This is the maximum relationship that the vehicle can have for when it brakes to stop at the given distance