Question

let x and y be transitive g-sets (ie g acts on either with a single orbit). show they are isomorphic, as g-sets iff we can find x in x, y in y, with equal stabilizers,

Answer 1

Two transitive g-sets, x and y, are isomorphic as g-sets if and only if we can find an element x in x and an element y in y such that they have equal stabilizers.

To prove this, we need to show two directions:

1. If x and y are isomorphic as g-sets, then we can find x in x and y in y with equal stabilizers.

- Let f: x -> y be an isomorphism between x and y as g-sets. Since x and y are transitive, there exists an element x0 in x and an element y0 in y such that f(x0) = y0. We can define the stabilizers of x0 and y0 as Stab(x0) and Stab(y0), respectively. Since f is an isomorphism, it preserves the stabilizers, meaning Stab(x0) = Stab(y0).

2. If we can find x in x and y in y with equal stabilizers, then x and y are isomorphic as g-sets.

- Let x0 be an element in x and y0 be an element in y such that Stab(x0) = Stab(y0). We can define a function f: x -> y as f(gx0) = gy0 for all g in G, where G is the group acting on x and y. This function f is well-defined because if gx0 = hx0 for some g,h in G, then g^(-1)h stabilizes x0, which implies
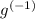`g^{(-1)`h is in Stab(x0) = Stab(y0). Therefore, f is a bijection since it has an inverse given by
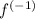`f^{(-1)`(gy0) = gx0. Moreover, f preserves the group action since f(gx0 * g') = f(g(g'x0)) = gg'y0 = gf(x0 * g') for all g,g' in G.

Two transitive g-sets, x and y, are isomorphic as g-sets if and only if we can find x in x and y in y with equal stabilizers.