Question

Compute the flux of the vector field F=8x²y²zk through the surface S which is the cone √x²+y²+ with 0≤z≤ R, oriented downward. Parameterize the cone using cylindrical coordinates.

Answer 1

The flux of F through the downward-oriented cone is
`-4\pi R^5/3`

We calculate the flux of the vector field F=8x²y²zk through the downward-oriented cone S defined by √(x²+y²) = z, 0 ≤ z ≤ R, using cylindrical coordinates.

Parameterization: In cylindrical coordinates, x = r cos(θ), y = r sin(θ), z = z. Substituting into the cone equation gives r = z, so the parameterization is:

v(r, θ) = (r cos(θ), r sin(θ), z)

Surface element: The surface element in cylindrical coordinates is dA = -r dz dθ (downward orientation).

Flux integral: The flux of F through S is given by the double integral:

∫∫S F · dA = ∫
`0^R` ∫
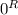`0^2`π 8
`r^4`
`cos^2`(θ)
`sin^2`(θ) z (-r dz dθ)

Integration: Evaluating the integral simplifies to:

`-4\pi R^5/3`

Therefore, the flux of F through the downward-oriented cone is
`-4\pi R^5/3`.