Due to the increase in market interest rates from 6% to 9%, you would expect to pay less than $10,000 for a bond that was initially issued at a lower interest rate. The exact amount you would be willing to pay can be determined by discounting the bond's future cash flows to their present value at the current market interest rate.
When considering the purchase of a bond one year before its maturity, several factors should be taken into account, especially if the market interest rates have changed since the bond was issued.
In this case, the local water company issued a $10,000 ten-year bond at a 6% interest rate, and you are thinking about buying it when there is only one year left until maturity, but the current market interest rate has risen to 9%.
a. With the increase in market interest rates to 9%, you would expect to pay less than $10,000 for this bond because existing bonds with lower interest rates become less valuable when new bonds are available that offer a higher return.
b. To calculate what you would actually be willing to pay for this bond, you need to discount the future cash flows (the $600 in interest due in one year, plus the $10,000 principal payment) back to the present value at the current market interest rate of 9%.
The equation to calculate the present value (PV) of a future cash flow (FV) is PV = FV /
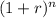 , where r is the discount rate and n is the number of periods until payment.
, where r is the discount rate and n is the number of periods until payment.
Using this formula, the present value of the bond is the sum of the present value of the interest payment and the principal repayment.