Question

A sample of students attending a large university has been selected. Is there a statistically significant difference between Liberal Arts majors and other students on average number of books (other than those required by course work) read per year? Use the five step model and write a sentence or two interpreting your results.

Liberal Arts Other
X₁= 16.2 X₂ = 13.7
s₁ = 2.3 s₂ = 9.0
N₁ = 236 N₂ = 321

Answer 1

The calculated two-sample t-test statistic is approximately t = 4.77. To determine statistical significance, compare |t| with the critical t-value for a two-tailed test at
`\(\alpha = 0.05\)`.

To determine if there is a statistically significant difference between Liberal Arts majors and other students in the average number of books read per year, a two-sample t-test is conducted using the following data:

Liberal Arts:

- Sample mean (X₁): 16.2

- Sample standard deviation (s₁): 2.3

- Sample size (N₁): 236

Other Students:

- Sample mean (X₂): 13.7

- Sample standard deviation (s₂): 9.0

- Sample size (N₂): 321

Using the five-step model for hypothesis testing:

Step 1: Formulate the hypotheses.

H₀:
`\mu_1` =
`\mu_2`

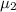
H₁:
`\mu_1`
`\\eq`
`\mu_2`

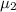
Step 2: Select the significance level
`(\(\alpha\))`.

`\[ \alpha = 0.05 \]`

Step 3: Select the test statistic and determine the critical region.

Using a two-sample t-test.

Step 4: Compute the test statistic.

`\[ t = \frac{(X₁ - X₂)}{\sqrt{\left((s₁^2)/(N₁)\right) + \left((s₂^2)/(N₂)\right)}} \]`

Now, substitute the given values:

`\[ t = \frac{(16.2 - 13.7)}{\sqrt{\left((2.3^2)/(236)\right) + \left((9.0^2)/(321)\right)}} \]`

`\[ t = \frac{2.5}{\sqrt{\left((5.29)/(236)\right) + \left((81.0)/(321)\right)}} \]`

`\[ t \approx (2.5)/(√(0.0224 + 0.2524)) \]`

`\[ t \approx (2.5)/(√(0.2748)) \]`

`\[ t \approx (2.5)/(0.5246) \]`

`\[ t \approx 4.77 \]`

Now, with this calculated t, you would compare it to the critical t-value for a two-tailed test with the given degrees of freedom and significance level
`(\(\alpha = 0.05\))`. If |t| is greater than the critical value, you would reject the null hypothesis.