Question

You have N boxes labeled Box 1,...,Box N. You have k balls. You drop the balls at random into boxes, independent of each other. For each ball the probability that it will land in a particular box is the same for all boxes, namely, t. Let Xį be the number of balls in Box 1 and Xn be the number of balls in Box N. Calculate Corr(X1, Xn). You must show derivations leading to your answer. Merely stating an expression will not receive any credits.

Answer 1

For randomly distributed balls among N boxes, the correlation
`\(\text{Corr}(X_1, X_N)\)`between
`\(X_1\)` and
`\(X_N\)` is 0. This implies no linear relationship between the number of balls in Box 1 and Box N.

The covariance between
`\(X_1\)` and
`\(X_N\)`can be calculated as:

`\[ \text{Cov}(X_1, X_N) = \text{E}(X_1X_N) - \text{E}(X_1)\text{E}(X_N) \]`

Given the probabilities for each ball to land in Box 1 or Box N are both
`\(1/N\)`,
`\(X_1\)` and
`\(X_N\)` follow a binomial distribution with parameters
`\(k\)` (number of balls) and \(p = 1/N\) (probability of success for each ball).

Therefore
`, \(\text{E}(X_1) = \text{E}(X_N) = kp = k/N\).`

Now, to find
`\(\text{E}(X_1X_N)\),` consider that the expected value of the product of two independent random variables is the product of their individual expected values:

`\(\text{E}(X_1X_N) = \text{E}(X_1)\text{E}(X_N)\)`

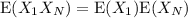
Substituting the values:

`\(\text{E}(X_1X_N) = (k/N)(k/N) = k^2/N^2\)`

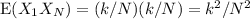
Now, plug these values into the covariance formula:

`\(\text{Cov}(X_1, X_N) = \text{E}(X_1X_N) - \text{E}(X_1)\text{E}(X_N) = (k^2)/(N^2) - (k)/(N) \cdot (k)/(N)\)`

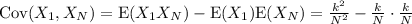
Simplify:

`\(\text{Cov}(X_1, X_N) = (k^2)/(N^2) - (k^2)/(N^2) = 0\)`

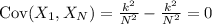
The covariance between
`\(X_1\)` and
`\(X_N\)`is zero, which implies they are uncorrelated.

Given the uncorrelated nature of
`\(X_1\)` and
`\(X_N\)`, the correlation coefficient between them is:

`\[ \text{Corr}(X_1, X_N) = \frac{\text{Cov}(X_1, X_N)}{\sqrt{\text{Var}(X_1) \cdot \text{Var}(X_N)}} \]`

Since the covariance is zero, the correlation coefficient will be zero as well.

Therefore, the correlation between
`\(X_1\)` and
`\(X_N\)`in this scenario where the balls are distributed uniformly at random among the boxes is zero.