The equation of the hyperbola is
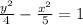 . Among the given options, the point (2.5, 3) lies on this hyperbola. Option B is correct.
. Among the given options, the point (2.5, 3) lies on this hyperbola. Option B is correct.
The standard form equation of a hyperbola with a vertical axis is given by:
![\[ ((y - k)^2)/(a^2) - ((x - h)^2)/(b^2) = 1 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ynaqs0cum37ai31347q0jgsxg0qf26hnh2.png)
where (h, k) is the center, a is the distance from the center to the vertices, and b is the distance from the center to the foci.
Given the vertices at (0, -2) and (0, 2), we can see that the center is at the origin (0,0). The distance from the center to the vertices is (a = 2).
The distance from the center to the foci is (c = 3).
The relationship between (a), (b), and (c) in a hyperbola is given by
 . Therefore,
. Therefore,
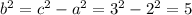 .
.
Now, plug these values into the equation:
![\[ (y^2)/(2^2) - (x^2)/(√(5)^2) = 1 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ni1hhiyi7fb6wcq2zzgqldkl4z47azats2.png)
Simplifying, we get:
![\[ (y^2)/(4) - (x^2)/(5) = 1 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/4fs88aq4jrynnfhh8d1c853q9taw3k9rep.png)
Now, let's check which point from the given options lies on this hyperbola.
a.
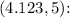
![\[ (5^2)/(4) - (4.123^2)/(5) \approx 1 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/30mirqppjuywj180ei8f2a688oed4vznw4.png) (approximately)
(approximately)
b.
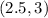 :
:
![\[ (3^2)/(4) - (2.5^2)/(5) = 1 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ju5ccrdeag8wxsxztltrftvzd7z8lzerjp.png)
c.
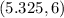 :
:
![\[ (6^2)/(4) - (5.325^2)/(5) \approx 1 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/fxcc83ukjo2h7nu9wuogp2aufmqkgpjmvk.png) (approximately)
(approximately)
d.
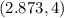 :
:
![\[ (4^2)/(4) - (2.873^2)/(5) \approx 1 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/5i0v90maxl1i2q2xt6cs935dyfcunkbqf4.png) (approximately)
(approximately)
So, the correct answer is (b)
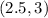 .
.