Question

A certain course has a freshmen, b sophomores, c juniors, and d seniors. Let X be the number of freshmen and sophomores (total), Y be the number of juniors, and Z be the number of seniors in a random sample of size n, where for Part (a) the sampling is with replacement and for Part (b) the sampling is without replacement (for both parts, at each stage the allowed choices have equal probabilities).

Find the joint PMF of X, Y,Z, for sampling with rep

Answer 1

For sampling with replacement, the joint PMF of X, Y, Z is
`\(P(X=x, Y=y, Z=z) = \binom{x+y+z}{x, y, z} \left((a)/(n)\right)^x \left((b)/(n)\right)^y \left((c)/(n)\right)^z \left((d)/(n)\right)^(n-(x+y+z))\)`. For sampling without replacement, a more complex hypergeometric-based expression is needed.

(a) Sampling with Replacement:

When sampling with replacement, the probability of selecting a particular class at each draw remains constant. The probability of selecting a freshman is
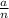`\( (a)/(n) \)`, a sophomore is
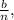`\( (b)/(n) \),` a junior is
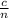`\( (c)/(n) \)`, and a senior is
`\( (d)/(n) \)`.

The joint PMF of X, Y, Z for sampling with replacement is given by:

`\[ P(X = x, Y = y, Z = z) = \binom{x+y+z}{x, y, z} \left((a)/(n)\right)^x \left((b)/(n)\right)^y \left((c)/(n)\right)^z \left((d)/(n)\right)^(n-(x+y+z)) \]`

Here,
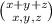`\( \binom{x+y+z}{x, y, z} \)` represents the multinomial coefficient.

(b) Sampling without Replacement:

When sampling without replacement, the probabilities change after each draw. Initially, the probabilities are
`\( (a)/(a+b+c+d) \)` for a freshman,
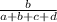`\( (b)/(a+b+c+d) \)` for a sophomore,
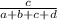`\( (c)/(a+b+c+d) \)` for a junior, and for a senior. However, the probabilities for subsequent draws will vary due to the reduction in the population size.

The joint PMF of X, Y, Z for sampling without replacement is relatively complex and depends on the specific distribution of freshmen, sophomores, juniors, and seniors. It involves the hypergeometric distribution since the probabilities change at each draw due to the lack of replacement.

The exact formula for the joint PMF in this scenario involves the hypergeometric probability function and the constraints of the problem but can be challenging to express in a simplified form due to the changing probabilities at each draw without replacement.

complete the question

A certain course has a freshmen, bsophomores, c juniors and d seniors. Let X be the number of freshmen and sophomores (total), Y be the number of juniors, and Z be the number of seniors in a random sample of sizen, where for Part (a) the sampling iswith replacement, and for Part (b) the sampling iswithout replacement (for both parts, at each stage the

A certain course has a freshmen, bsophomores, c juniors and d seniors. Let X be the

number of freshmen and sophomores (total), Y be the number of juniors, and Z be the number

of seniors in a random sample of sizen, where for Part (a) the sampling iswith replacement,

and for Part (b) the sampling iswithout replacement (for both parts, at each stage the allowed

choices have equal probabilities).

(a) Find the joint PMF of X, Y, Z, for sampling with replacement.

(b) Find the joint PMF of X, Y, Z, for sampling without replacement.