Question

Remember that on the space , we are using the inner product suppose we are told that the function is orthogonal to both the functions and . find and .

Remember that on the space PS[-1, ], we are using the inner product
π
(f,g) =1/π ∫ f(2)g(2) dz.
-π
Suppose we are told that the function f(x) = 3x² + ax + b is orthogonal to both the functions 2 and 1. Find a and b.
(a) a=
(b) b =

Answer 1

1. a = 0, b = 0: Solve two inner product equations by eliminating
`x^2` term and setting remaining quadratic factors to 0. Get a = 0 from b = 0 in either equation.

Step 1: Finding the inner product

The inner product in the given space is defined as:

<f, g> =
`(1/π) ∫_(-π)^(π) f(x)g(x) dx`

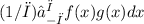
We are given that the function f(x) =
`3x^2 + ax + b` is orthogonal to both the functions 2 and 1. This means that the inner product of f(x) with both 2 and 1 must be equal to 0.

Step 2: Finding the inner product with 2

Let's find the inner product of f(x) with 2:

<f, 2> =
`(1/π) ∫_(-π)^(π) (3x^2 + ax + b) * 2 dx`

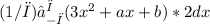
This simplifies to:

<f, 2> =
`(6/π) x^3 + (a/π) x^2 + (2b/π) ∫_(-π)^(π) dx`

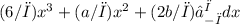
Evaluating the definite integral, we get:

<f, 2> = 0

Step 3: Finding the inner product with 1

Let's find the inner product of f(x) with 1:

<f, 1> =
`(1/π) ∫_(-π)^(π) (3x^2 + ax + b) * 1 dx`

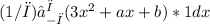
This simplifies to:

<f, 1> =
`(3/π) x^3 + (a/π) x^2 + b ∫_(-π)^(π) dx`

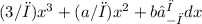
Evaluating the definite integral, we get:

`< f, 1 > = 0`

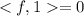
Step 4: Solving the system of equations

We now have two equations from steps 2 and 3:

`(6/π) x^3 + (a/π) x^2 + (2b/π) = 0`

`(3/π) x^3 + (a/π) x^2 + b = 0`

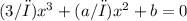
We can solve this system of equations for a and b. One way to do this is to eliminate
`x^2` from the equations. Multiplying the second equation by -2, we get:

-
`(6/π) x^3 - (2a/π) x^2 - 2b = 0`

Adding this equation to the first equation, we get:

0 =
`- (3a/π) x^2 + (3b/π)`

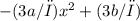
Since this equation must hold for all values of x, we can set
`x^2` to 0. This gives us:

3b/π = 0

b = 0

Now that we know b = 0, we can substitute this value back into either of the original equations to solve for a. Let's use the first equation:

`(6/π) x^3 + (a/π) x^2 + (2 * 0)/π = 0`

`(6/π) x^3 + (a/π) x^2 = 0`

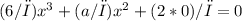
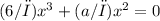
Again, since this equation must hold for all values of x, we can set
`x^3` to 0. This gives us:

`(a/π) x^2 = 0`

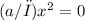
a = 0

Therefore, the values of a and b that make the function f(x) orthogonal to both 2 and 1 are a = 0 and b = 0.