None of the given vector fields is conservative because their curls are nonzero. Conservative vector fields have zero curl, ensuring independence of path in line integrals, a property crucial for potential functions.
To determine if a vector field is conservative, we need to check if its curl is zero. A vector field
 is conservative if and only if
is conservative if and only if
 is the curl operator.
is the curl operator.
If
 to be conservative is:
to be conservative is:
![\[(\partial N)/(\partial x) - (\partial M)/(\partial y) = 0\]](https://img.qammunity.org/2024/formulas/physics/high-school/f7zqy1o928n7b1lo3rez6i4bum9j31lyre.png)
Now, let's consider the vector fields given and determine which ones are conservative:
1.
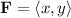
![\[\\abla * \mathbf{F} = (\partial)/(\partial x)(y) - (\partial)/(\partial y)(x) = 1 - (-1) = 2\]](https://img.qammunity.org/2024/formulas/physics/high-school/m8xgj7z1o9gf38sdrqk3l9bfwa9tc1u4qu.png)
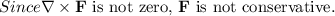
2.
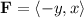
![\[\\abla * \mathbf{F} = (\partial)/(\partial x)(x) - (\partial)/(\partial y)(-y) = 1 - (-1) = 2\]](https://img.qammunity.org/2024/formulas/physics/high-school/uzqcy9tpxfinya2tztndxn0vju9g2qug9i.png)
Again,
 is not conservative.
is not conservative.
3.
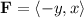 (same as above)
(same as above)
This vector field is not conservative for the same reason as in example 2.
4.

![\[\\abla * \mathbf{F} = (\partial)/(\partial x)(x) - (\partial)/(\partial y)(y) = 1 - (-1) = 2\]](https://img.qammunity.org/2024/formulas/physics/high-school/6qhzjzm42i7xr7ugkj1jmub06d7edfdued.png)
Once again,
 is not conservative.
is not conservative.
5.
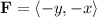
![\[\\abla * \mathbf{F} = (\partial)/(\partial x)(-x) - (\partial)/(\partial y)(-y) = -1 - 1 = -2\]](https://img.qammunity.org/2024/formulas/physics/high-school/ziuszeqs6i1sldaxgep0e6xuwkny4h602f.png)
This time,
 is not conservative.
is not conservative.
Since none of the given vector fields have a curl of zero, none of them are conservative. Conservative vector fields have the property that their curl is zero, and this property is necessary for the existence of a potential function. Without a potential function, the line integral of the vector field becomes path-dependent, leading to different values for different paths between the same endpoints.