The least squares regression line is ŷ = 38.75581x + 44.31395, where ŷ is the predicted ownership of company stock, and x is the years with the firm. The slope of 38.75581 suggests a yearly stock ownership increase of about 38.76 units.
To find the least squares regression line, we need to calculate the slope (b) and the y-intercept (a) using the following formulas:
![\[ b = \frac{\sum_(i=1)^(n) (x_i - \bar{x})(y_i - \bar{y})}{\sum_(i=1)^(n) (x_i - \bar{x})^2} \]\[ a = \bar{y} - b\bar{x} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ttvdarrgvqcwbejj3wxsmxtx2zvrojt9f0.png)
where:
- n is the number of data points (in this case, 8),
-
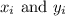 are the individual data points,
are the individual data points,
-
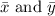 are the mean values of x and y respectively.
are the mean values of x and y respectively.
Let's calculate these values step by step:
1. Calculate the mean
![\[ \bar{x} = (6 + 12 + 14 + 6 + 9 + 13 + 15 + 9)/(8) = 10.5 \]\[ \bar{y} = (300 + 408 + 560 + 252 + 288 + 650 + 630 + 522)/(8) = 451.25 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/dorg6q4ea038bfqqff3xzhhb7hlbr9qz0a.png)
2. Calculate the slope
![\[ b = (\sum_(i=1)^(8) (x_i - 10.5)(y_i - 451.25))/(\sum_(i=1)^(8) (x_i - 10.5)^2) \]\[ b = ((6-10.5)(300-451.25) + (12-10.5)(408-451.25) + \ldots + (9-10.5)(522-451.25))/((6-10.5)^2 + (12-10.5)^2 + \ldots + (9-10.5)^2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/oocuesg7nmqj0bdp3wpilyjoi3oc4bux9q.png)
After calculating this expression, you should get b to be approximately 38.75581.
3. Calculate the y-intercept a:
![\[ a = 451.25 - 38.75581 * 10.5 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/m12nfjf8pfygisktqogv2f0skecl4sbl2h.png)
After calculating this expression, you should get a to be approximately 44.31395.
Therefore, the least squares regression line is:
![\[ \hat{y} = 38.75581x + 44.31395 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/5994641f1ggwiw14ne5acjvbuyokf8yqag.png)
Now, let's interpret the slope:
The slope of the regression line b represents the change in the dependent variable y for a one-unit change in the independent variable x. In this context, the slope of approximately 38.75581 means that, on average, for each additional year an employee spends with the firm x increases by 1, their ownership of company stock y is expected to increase by approximately 38.75581 units.