Question

Please I really need help on this​

Answer 1

A) x = 17

B) m∠LMN = 29°
m∠OMP = 61°

C) Not vertical angles.

Explanation:

Given angles:

• m∠LMN = (x + 12)°
• m∠OMP = (4x - 7)°

Part A

Complementary angles are two angles whose measures sum to 90°. Given that angle LMN and angle OMP are complementary angles, we can find the value of x by setting the sum of the two angles equal to 90° and solving for x:

`\begin{aligned}m\angle LMN + m\angle OMP&=90^(\circ)\\(x + 12)^(\circ) + (4x - 7)^(\circ)&=90^(\circ)\\x+12+4x-7&=90\\5x+5&=90\\5x+5-5&=90-5\\5x&=85\\5x / 5&=85 / 5\\x&=17\end{aligned}`

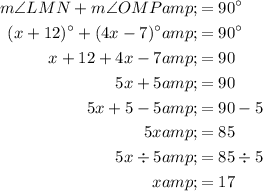
Therefore, the value of x is 17.

Part B

Now that we know the value of x, we can find the measures of angles LMN and OMP by substituting x = 17 into their expressions:

`\begin{aligned}m\angle LMN&=(x + 12)^(\circ)\\&=(17+12)^(\circ)\\&=29^(\circ)\end{aligned}`

`\begin{aligned}m\angle OMP&=(4x-7)^(\circ)\\&=(4(17)-7)^(\circ)\\&=(4(17)-7)^(\circ)\\&=68-7^(\circ)\\&=61^(\circ)\end{aligned}`

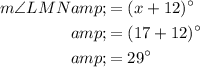
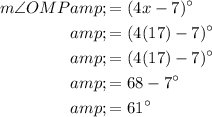
Therefore, m∠LMN = 29° and m∠OMP = 61°.

Part C

Vertical angles are a pair of non-adjacent angles formed by the intersection of two straight lines, and they are always congruent. Therefore, as angles LMN and OMP are not congruent, they cannot be vertical angles.