Question

Consider the air over a city to be a box that measures 100 km per side that reaches up to an altitude of 1.0 km. Wind (clean air) is blowing into the box along one of its sides with a speed of 4 m/s. An air pollutant is emitted into the box at a rate of 10.0 kg/s; the pollutant degrades with a rate constant k = 0.20/hr. a. Find the steady state concentration of the pollutant (µg/m3 ) in the box if the air is assumed to be completely mixed. b. If the wind speed suddenly drops to 1 m/s, estimate the concentration of the pollutant (µg/m3 ) two hours later.

Answer 1

a) ρ = 6.25 10⁵ μg / m³, b) ρ = 1 10⁷ μg / m³

Step-by-step explanation:

Let's analyze the exercise a little before starting, we must know the amount of pollutant in the box, that the one that enters less the one that degrades and with this value find the density or concentration.

Let's start by finding the volume of air that goes into the box

V = Lh x

Let's find the distance of air that enters per unit of time, as it goes at constant speed

x = v₀ t

we substitute

V₀ = Lh v₀ t

At this same time, a quantity of pollutant is distributed

Q₀ = r t

the contaminant that is entering reaches the entire box, therefore the total amount of contaminant is

Q = Qo t

we substitute

Q = r t²

the net amount of pollutant that remains is that less enters the one that degraded in the same time, as they ask for the steady state

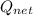`Q_(net)`= Q - k t

the pollutant concentration is

ρ = Q_net / V

V = L L h

ρ =
`(r \ t^2 - k \ t)/( L^2 h)`

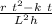
ρ =
`(r ( L^2)/(v_o^2) - k (L)/(v_o) ) (1)/(L^2 h)`

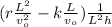
ρ =
`(r)/( v_o h) -(k)/(v_o L h)`

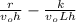
let's reduce the magnitudes to the SI system

r = 10 kg / s

L = 100 km = 100 10³ m

h = 1 km = 1 10³ m

k = dq / dt = 0.20 1/h ( 1h/3600 s) = 5.5555 10⁻⁵ 1/s

v₀ = 4 m / s

let's calculate

The volume of the box

V = (100 100 1) 109

V = 1 10¹³ m³

ρ =
`(10)/( 4^2 \ 1\ 10^3 ) - (5.5556 \ 10^(-5))/( 4 \ 100 \ 10^3 1 \ 10^3)`

ρ =
`6.25 10^(-4) - 1.389 ^(-13)`

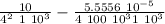
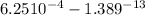
ρ = 6.25 10⁻⁴ kg / m³

let's reduce to μg / m³

ρ = 6.25 10⁻⁻⁴ kg / m³ (10⁹ μg / 1kg)

ρ = 6.25 10⁵ μg / m³

b) in case the air speed decreases to v₀ = 1 m / s

ρ= \frac{10}{ 1^2 \ 1\ 10^3 } - \frac{5.5556 \ 10^{-5}}{ 1 \ 100 \ 10^3 1 \ 10^3}

ρ = 1 10⁻² - 5.5556 10⁻¹³

ρ = 1 10⁻² kg / m³

ρ = 1 10⁷ μg / m³