Question

1.) (6 points) Find the cost of an ice cream and the cost of a soft drink.

The total cost of one ice cream and three soft drinks at Catherine's shop is $9

The total cost of two ice creams and five soft drinks is $16.

Let x be the cost of an ice cream and y be the cost of a soft drink.

Cost of Ice Cream

Cost of a Soft Drink

Answer 1

y=2 x=3

Explanation:

x+3y=9

2x+5y=16

let x have the same coefficient of 2

2x+6y=18

2x+5y=16

subtract the two values of x leaving

y=2

substitute y to get x in the original equation of

x+3y=9

×+3(2)=9

x=9-6

x=3

Answer 2

Cost of an ice cream = $3

Cost of a soft drink = $2

Explanation:

Let's set up a system of equations based on the given information:

Let
`\sf x` be the cost of an ice cream and
`\sf y` be the cost of a soft drink.

The first equation represents the total cost of one ice cream and three soft drinks:

`\sf x + 3y = 9`

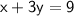
The second equation represents the total cost of two ice creams and five soft drinks:

`\sf 2x + 5y = 16`

Now, we have a system of two equations:

`\sf \begin{cases} x + 3y = 9 \\ 2x + 5y = 16 \end{cases}`

We can solve this system of equations to find the values of
`\sf x` and
`\sf y`.

Here's one way to solve it:

Multiply the first equation by 2 to make the coefficients of
`\sf x` in both equations match:

`\sf \begin{cases} 2x + 6y = 18 \\ 2x + 5y = 16 \end{cases}`

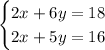
Now, subtract the second equation from the first to eliminate
`\sf x`:

`\sf \begin{cases} 2x + 6y - (2x + 5y) = 18 - 16 \\ y = 2 \end{cases}`

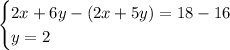
Now that we have the value for
`\sf y`, substitute it back into one of the original equations. Let's use the first equation:

`\sf x + 3(2) = 9`

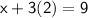
Solve for
`\sf x`:

`\sf x + 6 = 9`

`\sf x = 3`

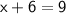
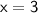
So, the cost of an ice cream (
`\sf x`) is $3.

The cost of a soft drink (
`\sf y`) is $2.