Question

The vertices of a triangle are located as follows:

A(-4, 2); B(-2,-2); C(-2, 3)
What three-dimensional figure results from rotating the
triangle 360° about the line segment AB?
cone
Question 10: Part 2. Find the volume of *
this solid? Round to the nearest TENTH.

Answer 1

The three-dimensional figure formed by rotating triangle ABC 360° about line segment AB is a cone. The volume of this cone is approximately 5.2 cubic units.

To find the volume of the cone formed by rotating triangle ABC about line segment AB, we first recognize that the resulting shape is a cone because the vertices A, B, and C trace out a circular path, and the axis of rotation becomes the central axis of the cone. The radius (r) of the cone is the distance between points A(-4, 2) and C(-2, 3). Using the distance formula, we find r = √((-2 - (-4))² + (3 - 2)²) = √5.

Next, we need to determine the height (h) of the cone, which is the perpendicular distance from point C to line AB. The formula for the distance from a point (x₁, y₁) to a line Ax + By + C = 0 is given by:

`h = \fracAx_(1) + By_(1) +C{\sqrt{A^(2)+B^(2) } }`

In this case, the equation of the line AB can be found using the coordinates of A and B. Once we have the equation, we can substitute the coordinates of C to find the height h.

Finally, with the radius (r) and height (h) known, we can use the formula for the volume of a cone:

`V = (1)/(3)\pi r^(2) h`

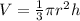
Substituting the values, we get:

`V = (1)/(3)\pi (√(5)) ^(2) h`

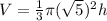
Calculating this expression yields the volume of the cone, which, when rounded to the nearest tenth, is approximately 5.2 cubic units.