Question

HELPP!!!!!!! Problem is in photo

Answer 1

13,556 N

Step-by-step explanation:

We are given:

• m = 2150 kg
• L = 8.74 m
• θ = 51.0°

To solve for the force that the chain exerts on a drawbridge, we'll apply principles of static equilibrium. This is where the sum of moments and forces acting on the bridge add to zero, since there is no rotation. I have attached an image for you to view, I used this as reference. Taking the sum of moments about point 'o':

`\sum M_o: \vec T L\sin (\theta)-\vec w\left((L)/(2)\right)=0`

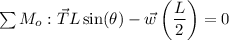
Recall,

• Clockwise torques are negative
• Counter-clockwise torques are positive

Plug in our values and solve for 'T':

`\Longrightarrow \vec T L\sin (\theta)-\vec w\left((L)/(2)\right)=0\\\\\\\\\Longrightarrow \vec T L\sin (\theta)-mg\left((L)/(2)\right)=0\\\\\\\\\Longrightarrow \vec T(8.74 \text{ m})\sin (51.0 \textdegree)-(2150 \text{ kg})(9.8 \text{ m/s$^2$})\left(\frac{8.74 \text{ m}}{2}\right)=0\\\\\\\\\Longrightarrow \vec T(8.74 \text{ m})\sin (51.0 \textdegree)=(2150 \text{ kg})(9.8 \text{ m/s$^2$})\left(\frac{8.74 \text{ m}}{2}\right)\\\\\\\\`

`\Longrightarrow \vec T=\frac{(2150 \text{ kg})(9.8 \text{ m/s$^2$})\left(\frac{8.74 \text{ m}}{2}\right)}{(8.74 \text{ m})\sin (51.0 \textdegree)}\\\\\\\\\therefore \vec T =\boxed{13,556\text{ N}}`

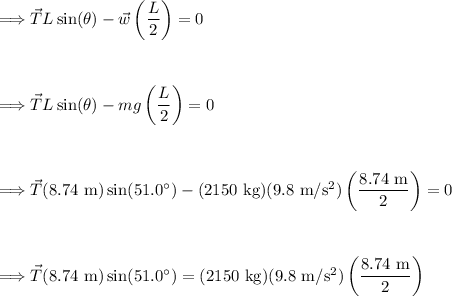
Thus, the chain exerts a force of 13,556 Newtons to hold up the drawbridge.