The recursive formulas arranged in order from least to greatest are;
aₙ₊₁ = -5 + aₙ
↓
aₙ₊₁ = (-1/2)·aₙ
↓
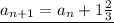
↓
aₙ₊₁ = 2·aₙ
The steps used to find the correct order of the recursive formula can be presented as follows;
The 10th term of the recursive formula aₙ₊₁ = aₙ +
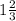 is found as follows;
is found as follows;
a₉₊₁ = a₉ +
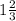
a₂ = a₁ +
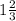
a₃ = a₂ +
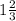
a₂ +
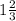 = a₁ +
= a₁ +
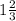 +
+
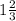
a₃ = a₁ + 2 ×
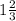
a₃ = a₁ + (3 - 1) ×
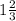
Similarly, a₉₊₁ = a₁ + (10 - 1) ×
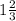
a₁₀ = -7
 + (10 - 1) ×
+ (10 - 1) ×
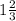
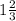 = 5/3
= 5/3
-7
 = -23/3
= -23/3
a₁₀ = (-23/3) + (10 - 1) × (5/3)
(-23/3) + (10 - 1) × (5/3) = 22/3
a₁₀ = 22/3
Similarly, we get; The 10th term of the formula aₙ₊₁ = -5 + aₙ, where a₁ = 32 is; a₁₀ = (10 - 1) × (-5) + 32
(10 - 1) × (-5) + 32 = -13
a₁₀ = -13
The formula aₙ₊₁ = 2·aₙ is a geometric progression, with the 10th term being a₁₀ = 2¹⁰ × a₁
The 10th term of the formula aₙ₊₁ = 2·aₙ, with a₁ = 0.125 is therefore;
a₁₀ = 2¹⁰ × 0.125
2 ¹⁰ × 0.125 = 128
a₁₀ = 128
The formula aₙ₊₁ = (-1/2)·aₙ is a geometric progression, with the 10th term being; a₁₀ = (-1/2)¹⁰ × a₁
a₁ = 2,048, therefore;
a₁₀ = (-1/2)¹⁰ × 2048
a₁₀ = 2