Question

Rewrite the expression in the form \[k\cdot y^n\]. Write the exponent as an integer, fraction, or an exact decimal (not a mixed number). \[\left(4\sqrt[4]{y^5}\right)^{^{\scriptsize\dfrac{1}2}}=\]

Answer 1

The result obtained, when the expression,
`(4\sqrt[4]{y^5})^{(1)/(2)` is rewritten in the form of
`k\cdot y^n` is
`2\ \cdot\ y^{(5)/(8)}`

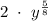
How to rewrite
`(4\sqrt[4]{y^5})^{(1)/(2)` in the form of
`k\cdot y^n`?

To rewrite the expression,
`(4\sqrt[4]{y^5})^{(1)/(2)` in the form of
`k\cdot y^n`, we must first simplify the given expression to look exactly as
`k\cdot y^n`. This is illustrated below:

• Expression given from the question:
  `(4\sqrt[4]{y^5})^{(1)/(2)`
• Rewritten expression in the form of
  `k\cdot y^n` =?

Applying the laws of indices, to simplify the expression, we have:

`(4\sqrt[4]{y^5})^{(1)/(2)}\\\\4^{(1)/(2)}\ \cdot\ (\sqrt[4]{y^5})^{(1)/(2)}\\\\4^{(1)/(2)}\ \cdot\ (y^{(5)/(4)})^{(1)/(2)}\\\\2\ \cdot\ y^{(5)/(8)}`

From the above, we can conclude that the expression from the question when expressed in
`k\cdot y^n` is
`2\ \cdot\ y^{(5)/(8)}`

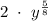
Complete question:

See attached photo