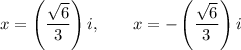Question

Can someone please help me with the problem? Please show your work.

Directions: Solve the following. Which is a solution to 3x^2 + 2 =0?

(√6/3)i

2/3

1

(2/3)i

​

Answer 1

Explanation:

`\boxed{i=√(-1) }`

`3x^(2) +2=0`

`3x^(2) =-2`

`x^(2) =-(2)/(3)`

`x=\sqrt{-(2)/(3) }`

`=\sqrt{(2)/(3) } *√(-1)`

`=\sqrt{(2)/(3) } \ i`

Answer 2

`x = \left((√(6))/(3)\right) i`

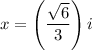
Explanation:

To solve the quadratic equation 3x² + 2 = 0, we can use the quadratic formula, which is given by:

`x = (-b \pm √(b^2 - 4ac))/(2a)`

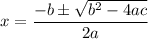
In the case of 3x² + 2 = 0, we have:

• 
  `a = 3`
• 
  `b = 0`
• 
  `c = 2`

Plug these values into the quadratic formula:

`x = (-0 \pm √((0)^2 - 4(3)(2)))/(2(3))`

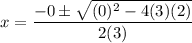
Simplify:

`x = (\pm √(-24))/(6)`

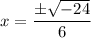
Since the part under the square root sign is negative, the solutions will be complex numbers.

Rewrite -24 as the product of 2² · 6 · (-1):

`x = (\pm √(2^2 \cdot 6 \cdot (-1)))/(6)`

`\textsf{Apply the radical rule:} \quad √(ab)=\sqrt{\vphantom{b}a}√(b)`

`x = (\pm √(2^2) √(6) √(-1))/(6)`

`\textsf{Apply the radical rule:} \quad √(a^2)=a, \quad a \geq 0`

`x = (\pm 2 √(6) √(-1))/(6)`

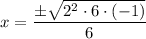
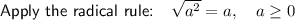
Divide the numerator and denominator by the common factor 2:

`x = (\pm √(6) √(-1))/(3)`

`\textsf{Apply the imaginary number rule:} \quad √(-1)=i`

`x = (\pm √(6) \:i)/(3)`

`x = \pm \left((√(6))/(3)\right) i`

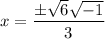
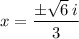
So, the solutions to the equation 3x² + 2 = 0 are:

`x = \left((√(6))/(3)\right) i, \qquad x=-\left((√(6))/(3)\right) i`