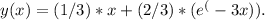Final answer:
The function y(x) for the initial value problem y' = x-3y with
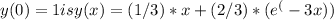
 on y(0) = 1 into the integral equation, we can solve for the constant of integration C and find the specific function y(x).
on y(0) = 1 into the integral equation, we can solve for the constant of integration C and find the specific function y(x).
Step-by-step explanation:
To solve the initial value problem y' = x-3y with y(0) = 1:
(a) We can find a function y(x) by solving the differential equation. Rearranging the equation, we get y' + 3y = x. To solve this, we can use an integrating factor. The integrating factor is e^(3x). Multiply the entire equation by this factor to get
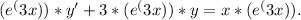
 h respect to x to obtain
h respect to x to obtain
 gration. Divide both sides by (e^(3x)) to solve for y and we get
gration. Divide both sides by (e^(3x)) to solve for y and we get
 ) = 1, we substitute x = 0 and y = 1 into the equation to find the value of C. Solving for C, we get C = 2/3. Therefore, the function y(x) is
) = 1, we substitute x = 0 and y = 1 into the equation to find the value of C. Solving for C, we get C = 2/3. Therefore, the function y(x) is
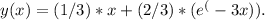
(b) The equivalent integral equation for this problem is
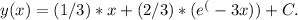
(c) To solve the equivalent integral equation, we can use the initial condition y(0) = 1. Substitute x = 0 and y = 1 into the equation to find the value of C. Solving for C, we get C = 2/3. Therefore, the function y(x) is