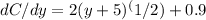Final answer:
To find dC/dy, differentiate each term in the consumption function individually using the power rule and constant rule.
Step-by-step explanation:
To find dC/dy, the derivative of the consumption function with respect to national disposable income, we will differentiate each term in the function individually:
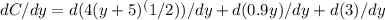
Applying the power rule and the constant rule, we get:
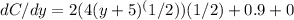
Simplifying further: