Question

Find the inverse Laplace transform L⁻¹{F(s)} of the given function.

F(s)=8s²-6s+18/s(s²+9)
Your answer should be a function of t.
L⁻¹{F(s)} = ____

Answer 1

The inverse Laplace transform of F(s) = 8s²-6s+18/s(s²+9) is L⁻¹{F(s)} = 2 - 2cos(3t) + sin(3t).

Step-by-step explanation:

To find the inverse Laplace transform of F(s), we need to express F(s) in the form of a standard Laplace transform pair. We can break down F(s) into partial fractions: F(s) =
`2/s - (4s-2)/(s^2+9) + 2s/(s^2+9).`

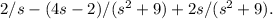
Next, we can use the table of Laplace transforms to find the inverse Laplace transform of each term. The inverse Laplace transforms of
`1/s, 1/(s^2+9), and s/(s^2+9) are 1, sin(3t),`
`1/s, 1/(s^2+9), and s/(s^2+9) are 1, sin(3t),`

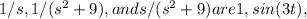
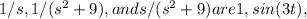
Therefore, the inverse Laplace transform of F(s) is L⁻¹{F(s)} = 2 - 2cos(3t) + sin(3t).