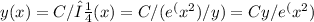Question

Find the general solution of the differential equation: dy + (2xy-4e⁻ˣ²)dx = 0.

What is the integrating factor? μ(x) = ________
Use lower case c for the constant in answer below
y(x) = ________

Answer 1

To find the general solution of the given differential equation, we can use an integrating factor. The integrating factor in this case is e^(x^2) / y. Multiplying the differential equation by the integrating factor and integrating both sides gives the general solution as
`y(x) = Cy / e^(x^2)` constant of integration.

Step-by-step explanation:

To find the general solution of the differential equation, we can use an integrating factor. In this case, the integrating factor, denoted as μ(x), is determined by the coefficient of dx, which is (2xy - 4e^(-x^2)). To find μ(x), we divide the coefficient by y and take the antiderivative with respect to x. This gives us
`μ(x) = e^(x^2) / y.`

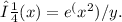
Multiplying the given differential equation by μ(x), we get
`μ(x)dy + (2xye^(x^2) - 4e^0)dx = 0`the equation is the derivative of (y * μ(x)) with respect to x. Therefore, integrating both sides gives us y(x) * μ(x) = C, where C is the constant of integration. Solving for y(x), we have:

`y(x) = C / μ(x) = C / (e^(x^2) / y) = Cy / e^(x^2)`