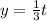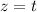Answer:

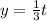
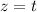
Step-by-step explanation:
Given
 at
at
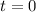
Point:
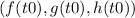
 ,
,
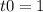 -- Missing Information
-- Missing Information
Required
Determine the parametric equations

Differentiate with respect to t
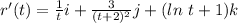
Let t = 1 (i.e
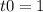 )
)
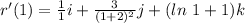
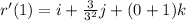
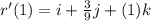
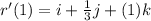
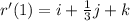
To solve for x, y and z, we make use of:

This implies that:

So, we have:
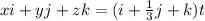
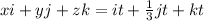
By comparison:
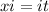
Divide by i

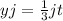
Divide by j
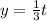
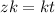
Divide by k
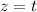
Hence, the parametric equations are: