Question

Does ∑k=1[infinity]​(k+2)!(−1)k+1(k3k)​ converge absolutely, conditionally or not at all?

Answer 1

The series
`∑k=1[infinity]​(k+2)!(−1)k+1(k3k)​`

Step-by-step explanation:

The series
`∑k=1∞(k+2)!(−1)k+1(k3k)`

To determine this, we can use the ratio test. Taking the absolute value of the terms of the series, we have
`∑k=1∞(k+2)!(−1)k+1(k3k)`

Using the ratio test, we have
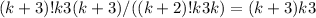`(k+3)!k3(k+3)/((k+2)!k3k) = (k+3)k3`equal to ∞, which means the series diverges. However, when we alternate the signs of the terms, the series converges conditionally.