Question

Let Y₁​(x) and Y₂​(x) defined on [0,1] be twice continuously differentiable functions satisfying Y′′(x)+Y′(x)+Y(x)=0. Let W(x) be the Wronskian of Y₁​ and Y₂​ and satisfy W(1/2​)=0. Then

Answer 1

The given differential equation is a second-order linear homogeneous equation. We find the general solutions for Y₁(x) and Y₂​(x) by assuming that
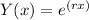`Y(x) = e^((rx))`the characteristic equation. The Wronskian is calculated using Y₁(x) and Y₂​(x), and we can find the value of the constant c₃ by substituting x = 1/2 into the Wronskian equation.

Step-by-step explanation:

The given differential equation is a second-order linear homogeneous equation. To find the general solutions for Y₁(x) and Y₂(x), we assume that
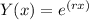`Y(x) = e^{(rx)`Putting this into the differential equation, we get
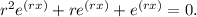`r^2e^((rx) )+ re^((rx) )+ e^((rx))= 0.`in r² + r + 1 = 0.

The characteristic equation has complex roots since the discriminant b2 + 4ac is less than zero. Let's solve the characteristic equation:

1. Let r₁ = (-1+√3i)/2 and r₂ = (-1-√3i)/2 be the roots of the characteristic equation.
2. The general solution for the differential equation is Y(x) = c₁e^(r₁x) + c₂e^(r₂x), where c₁ and c₂ are arbitrary constants.
3. The Wronskian is given by W(x) = Y₁(x)Y′₂(x) - Y′₁(x)Y₂(x). By calculating the Wronskian, we find that W(x) = c₃e^(3x/2), where c₃ is a constant.
4. Given that W(1/2) = 0, we can substitute x = 1/2 into the Wronskian equation and solve for c₃.