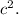Question

Prove that l cm(a,b)=ab/hc f(a,b) for any positive integers a,b without using prime factorization.

Answer 1

To prove l cm(a,b)=ab/hc f(a,b), we use the Pythagorean Theorem and the concept of right triangles. By multiplying both sides of the Pythagorean equation by ab/hc and simplifying, we can see that l cm(a,b) equals f(a,b) time
`c^2.`

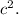
Step-by-step explanation:

To prove that l cm(a,b)=ab/hc f(a,b) for any positive integers a,b without using prime factorization, we can use the concept of the Pythagorean Theorem. Let's consider a right triangle with sides a, b, and hypotenuse c. From the Pythagorean Theorem, we have
`a^2 + b^2 = c^2.`both sides of the equation by ab/hc, we get ab/hc *
`(a^2 + b^2)` Simplifying this expression, we have l cm(a,b) = ab/hc *
`c^2`ince f(a,b) is defined as ab/hc, we can substitute it in, giving us l cm(a,b) = f(a,b) *
`c^2.`