Question

Given the second order initial value problem y"−16y=8δ(t−5), y’(0)=1, y’(0)=28 Let Y(s) denote the Laplace transform of y. Then Y(s)=____________ Taking the inverse Laplace transform we obtain y(t)=__________

Answer 1

To solve the given second-order initial value problem, we can use Laplace transforms. After finding the Laplace transform of y and applying the initial conditions, we can use inverse Laplace transform to find y(t).

Step-by-step explanation:

To solve the given second-order initial value problem using Laplace transforms, we need to find the Laplace transform of y and then apply the initial conditions to find the inverse Laplace transform. Let's solve step by step:

Step 1: Take the Laplace transform of the given differential equation:

`Y(s) - s²Y(s) - 16Y(s) = 8e^(-5s)`

Step 2: Solve for Y(s):

`Y(s)(1 - s² - 16) = 8e^(-5s)`

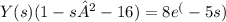
Y(s) = 8e^(-5s) / (1 - s² - 16)

Step 3: Apply the initial conditions:

`Y(s) = y(0) + sY(s) - y'(0)`

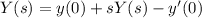
1 = 0 + sY(s) - 28

Y(s) = (29 - s) / (1 - s² - 16)

Step 4: Take the inverse Laplace transform to get y(t):

y(t) = L^-1{Y(s)}

To find the inverse Laplace transform, we need to apply partial fraction decomposition and use the table of Laplace transforms.