Question

Let B = {(1, 2), (-1,-1)) and B' {(-4,1), (0, 2)) be bases for R2, and let 0 2 A= be the matrix for T: R2R relative to B.

(a) Find the transition matrix P from B' to B P=
(b) Use the matrices P and A to find [vlB and [T(v)ls, where 10
(c) Find P- and A'(the matrix for T relative to B)
(d) Find [T v)la two ways. 19

Answer 1

To find the transition matrix P, the coordinates of a vector v, and the matrix A' for T relative to B, we use the formulas P * B' = B, [v]B = P * [v]B', [T(v)]B = A * [v]B, A
`' = P^-1 * A * P`A' * [v]B.

Step-by-step explanation:

To find the transition matrix P from B' to B, we need to find the matrix that transforms the basis vectors of B' to the basis vectors of B. Let's call the transformation matrix P. We can find P by solving the equation P * B' = B, where B' is the matrix whose columns are the basis vectors of B' and B is the matrix whose columns are the basis vectors of B.

Once we have P, we can use it to find [v]B, which represents the coordinates of a vector v in the basis B, by calculating [v]B = P * [v]B'. To find [T(v)]B, which represents the coordinates of the transformed vector T(v) in the basis B, we calculate [T(v)]B = A * [v]B, where A is the matrix for T: R2->R2 relative to B.

To find P^-1, the inverse of P, we can solve the equation
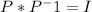`P * P^-1 = I` the identity matrix. Once we have P^-1, we can find A', the matrix for T relative to B, by calculating
`A' = P^-1 * A * P.`

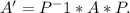
To find [T(v)]B directly, we can use the formula [T(v)]B = A' * [v]B. This gives us the coordinates of T(v) in the basis B.