Question

For 1st order ODE below y'=2y−3t; y(0)=1

The exact solution can be found is y(t)= 3t/2+3/4+e²ᵗ/4
(a) Use the fourth order Runge-Kutta method with a step-size of 0.01 to compute an approximate value for the solution at t=0.4.
(b) Find the percentage error between the fourth order Rung-Kutta method and the exact solution.

Answer 1

The fourth order Runge-Kutta method can be used to compute an approximate value for the solution at t=0.4. The percentage error can be found by comparing the approximate solution with the exact solution.

Step-by-step explanation:

To compute an approximate value for the solution at t=0.4 using the fourth order Runge-Kutta method, we can follow these steps:

1. Start with the initial condition y(0) = 1.
2. Compute the slope at t=0 using the given differential equation:
   `y'(t) = 2y - 3t`itial condition to find the slope:
   `y'(0) = 2(1) - 3(0) = 2.`
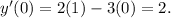
3. Using the slope computed in the previous step, find the values of k1, k2, k3, and k4 as follows:
4. k1 = h * y'(t)
5. k2 = h * y'(t + h/2)
6. k3 = h * y'(t + h/2)
7. k4 = h * y'(t + h)
8. Compute the average slope by adding k1, k2, k3, and k4 and dividing by 6: y_new = y_old + (k1 + 2k2 + 2k3 + k4)/6
9. Repeat steps 3-4 for the desired number of iterations, in this case, t=0.4

The percentage error can be found by comparing the approximate solution obtained using the fourth order Runge-Kutta method with the exact solution. Subtract the approximate value from the exact value and divide by the exact value, then multiply by 100 to get the percentage error.