Question

​Using Laplace Transforms determine the solution y(t), to the following initial value problem

d y/d t-4 y=-7 H(t-2),
subject to the boundary condition
y(0)=-4

Answer 1

To solve the given initial value problem using Laplace transforms, apply the Laplace transform to both sides of the differential equation. Substitute the initial condition and solve for Y(s). Finally, take the inverse Laplace transform of Y(s) to obtain y(t).

Step-by-step explanation:

Using Laplace Transforms to Solve the Initial Value Problem

To solve the given initial value problem using Laplace transforms, we first need to apply the Laplace transform to both sides of the differential equation. The Laplace transform of dy/dt is sY(s) - y(0), where Y(s) is the Laplace transform of y(t). The Laplace transform of y(t) is denoted as Y(s) as well.

After applying the Laplace transform, the given differential equation becomes:

`sY(s) - y(0) - 4Y(s) = -7e^(-2s)`

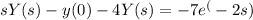
Next, we substitute the initial condition y(0) = -4 into the equation and solve for Y(s). Once we have the value of Y(s), we can find y(t) by taking the inverse Laplace transform of Y(s).