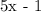Question

Simplify
2^(log(2)10x^5-log(2)2x)

Answer 1

To simplify the expression

`2^(log(2)10x^5-log(2)2x),`es of logarithms and exponents. The expression simplifies to 5x - 1.

Step-by-step explanation:

To simplify the given expression, we can use the properties of logarithms and exponents. Remember that the logarithm of a product of two numbers is the sum of the logarithms of the two numbers. Also, the logarithm of the number resulting from the division of two numbers is the difference between the logarithms of the two numbers. Let's break down the expression step by step:

1. Using the property of the logarithm of a product, we can rewrite the expression as:

`$$2^{\log_2{(10x^5)}} - \log_2{(2x)}$$`

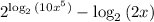
1. Since the base of the logarithm is 2, the logarithm of 2 to the base 2 is equal to 1. So the expression becomes:

`$$2^{\log_2{(10x^5)}} - 1 - \log_2{(2x)}$$`

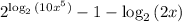
1. Using the property of the logarithm of a division, we can rewrite the expression as:

`$$2^{\log_2{(10x^5/(2x))}} - 1$$`

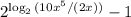
1. Simplifying the expression inside the logarithm:

`$$2^{\log_2{(5x)}} - 1$$`

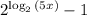
1. Finally, using the property of exponentiation, we can simplify the expression as:

`$$5x - 1$$`

Answer 2

5x

Step-by-step explanation:

`2^{log_2(10x^5)-log_2(2x)`

`=2^{log_2((10x^5)/(2x))}`

`=2^(log_2(5x))`

`\boxed{a^(log_a(b))=b}`

Therefore

`2^(log_2(5x))=5x`