Question

A crate rests on a flatbed truck which is initially traveling at 17.9 m/s on a level road. The driver applies the brakes and the truck is brought to a halt in a distance of 46.1 m. If the deceleration of the truck is constant, what is the minimum coefficient of friction between the crate and the truck that is required to keep the crate from sliding

Answer 1

The minimum coefficient of friction required is 0.35.

Step-by-step explanation:

The minimum coefficient of friction required to keep the crate from sliding can be found as follows:

`-F_(f) + F = 0`

`-F_(f) + ma = 0`

`\mu mg = ma`

`\mu = (a)/(g)`

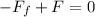
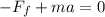
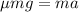
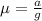
Where:

μ: is the coefficient of friction

m: is the mass of the crate

g: is the gravity

a: is the acceleration of the truck

The acceleration of the truck can be found by using the following equation:

`v_(f)^(2) = v_(0)^(2) + 2ad`

`a = (v_(f)^(2) - v_(0)^(2))/(2d)`

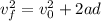
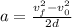
Where:

d: is the distance traveled = 46.1 m

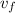`v_(f)`: is the final speed of the truck = 0 (it stops)

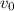`v_(0)`: is the initial speed of the truck = 17.9 m/s

`a = (-(17.9 m/s)^(2))/(2*46.1 m) = -3.48 m/s^(2)`

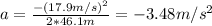
If we take the reference system on the crate, the force will be positive since the crate will feel the movement in the positive direction.

`\mu = (a)/(g)`

`\mu = (3.48 m/s^(2))/(9.81 m/s^(2))`

`\mu = 0.35`

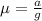
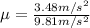
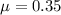
Therefore, the minimum coefficient of friction required is 0.35.

I hope it helps you!