Question

Answer the following questions on your paper. Label each problem. Submit your work in this question. (5 points each) 1. Simplify the expression:

1−sin2tsin2t⋅cot2t​
2. Verify the identity: secθsecθ−cosθ​=sin2θ
3. Verify the identity: sec2θ−sin2θsec2θ=1

Answer 1

1. Simplify the expression:

`\[ (1 - \sin^2(t))/(\sin^2(t) \cdot \cot^2(t)) = \csc^2(t) \]`

2. Verify the identity:

`\[ \sec(\theta)\left(\sec(\theta) - \cos(\theta)\right) = \sin^2(\theta) \]`

3. Verify the identity:

`\[ \sec^2(\theta) - \sin^2(\theta)\sec^2(\theta) = 1 \]`

Step-by-step explanation:

1. To simplify the given expression, we start by using the Pythagorean identity
`\(\sin^2(t) + \cos^2(t) = 1\) to rewrite \(1 - \sin^2(t)\) as \(\cos^2(t)\).` Substituting this into the expression, we get
`\((\cos^2(t))/(\sin^2(t) \cdot \cot^2(t))\).`Using the reciprocal identity
`\(\cot(t) = (1)/(\tan(t)) = (\cos(t))/(\sin(t))\), we simplify further to \(\csc^2(t)\).`

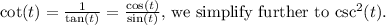
2. For the identity verification, we begin with the left side
`\(\sec(\theta)(\sec(\theta) - \cos(\theta))\).` Applying the definition
`\(\sec(\theta) = (1)/(\cos(\theta))\)`, we simplify and manipulate terms to eventually obtain
`\(\sin^2(\theta)\)`, which matches the right side of the identity.

3. To verify the second identity, we start with the left side
`\(\sec^2(\theta) - \sin^2(\theta)\sec^2(\theta)\).` Using the Pythagorean identity and simplifying, we arrive at the right side (1), confirming the identity.

In summary, the simplification involves utilizing trigonometric identities and basic algebraic manipulations. The identity verifications require applying definitions, trigonometric identities, and algebraic simplifications, ensuring that equality holds.