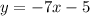Final answer:
The equation of the tangent line to the graph of f(x) at the point (0, -5) is y = -7x - 5.
Step-by-step explanation:
The tangent line to the graph of f(x) at the point (0, -5) can be found by finding the first derivative of f(x) and evaluating it at x = 0. The slope of the tangent line is equal to the value of the first derivative at that point, which represents the rate of change of the function at that point.
- Find the derivative of
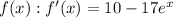
- Evaluate the derivative at
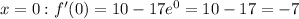
- The slope of the tangent line is -7, so the equation of the line is y = -7x + b
- Substitute the coordinates of the given point (0, -5) into the equation to find the value of b: -5 = -7(0) + b, b = -5
- The equation of the tangent line is