Question

Let f(x)=7 x²-3 x.

(a) Find the derivative of the line tangent to the graph of f at x=4.
Slope at x=4 :
(b) Find an equation of the line tangent to the graph of f at z=4.
Tangent line: y=

Answer 1

The derivative of function f(x)=7x²-3x at x=4 is 53, which represents the slope of the tangent line at that point. The equation of the tangent line at x=4 is y=53x-112.

Step-by-step explanation:

To find the derivative of the function f(x) = 7x² - 3x, we use the power rule for derivatives. The derived function, f'(x), representing the slope of the tangent line at any point x, is calculated as:

`f'(x) = d/dx (7x²) - d/dx (3x) = 14x - 3.`

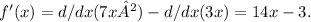
At x = 4, the slope is thus:

f'(4) = 14(4) - 3 = 56 - 3 = 53.

This slope represents the steepness of the tangent line at x = 4. To find the equation of the tangent line at x=4, we then use the point-slope form of a line, which is y - y1 = m(x - x1). We have the slope m = 53, and we need y1 which is the value of f(x) at x = 4:

`f(4) = 7(4)² - 3(4) = 7(16) - 12 = 112 - 12 = 100.`

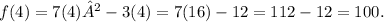
Therefore, the equation of the tangent line is:

`y - 100 = 53(x - 4).`

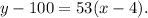
Simplifying, we get:

y = 53x - 212 + 100

y = 53x - 112.

Thus, the equation of the tangent line at x = 4 is y = 53x - 112.