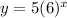Question

Write an exponential function to describe the given sequence of numbers, assuming that the first number in the sequence corresponds to x = 0.

5.30, 180, 1080, 6480...

Answer 1

`y = 5(6) {}^(x)`

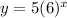
Explanation:

A exponential function is represented by

`y = ab {}^(x)`

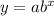
where a is the vertical stretch and b is the base and x is the nth

power of x

Since the first number corresponds with zero, that means our y intercept is the first number.

This means when x=0 , y=5 so let find the value of 5.

`5 = ab {}^(0)`

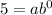
b to the 0th power equal 1 so

`5 = a * 1`

`a = 5`

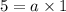
Our equation is for now

`y = 5b {}^(x)`

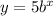
Now let plug in 1,30

`30 = 5b {}^(1)`

Divide 5 by both sides

`6 = b {}^(1)`

Anything to the 1st power is itself so b equal 6.

So our equation is

`y = 5(6) {}^(x)`