Final answer:
To solve the equation
 the variable x by taking the natural logarithm of both sides and subtracting 2. The approximate value of x is 0.3026.
the variable x by taking the natural logarithm of both sides and subtracting 2. The approximate value of x is 0.3026.
Step-by-step explanation:
To solve the equation
 and round to 4 decimal places, we need to isolate the variable x. We can start by taking the natural logarithm of both sides of the equation to get rid of the exponent. Using the property that ln(e^a) = a, we have:
and round to 4 decimal places, we need to isolate the variable x. We can start by taking the natural logarithm of both sides of the equation to get rid of the exponent. Using the property that ln(e^a) = a, we have:
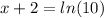
Next, we can subtract 2 from both sides of the equation to solve for x:
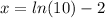
Using a calculator to evaluate ln(10) minus 2, we find that x is approximately 0.3026.