Question

An automobile manufacturer claims that its car has a 57.7 miles/gallon (MPG) rating. An independent testing firm has been contracted to test the MPG for this car since it is believed that the car has an incorrect manufacturer's MPG rating. After testing 210 cars, they found a mean MPG of 57.4. Assume the standard deviation is known to be 1.9. A level of significance of 0.1 will be used. Find the value of the test statistic. Round your answer to 2 decimal places.

Answer 1

The value of test statistic

|Z| = |-2.2883| = 2.2883

Explanation:

Step(i):-

Given that the mean of the Population = 57.7miles/gallon

The standard deviation of the Population = 1.9

The mean of sample x⁻ = 57.4

Given that the sample size 'n' =210

level of significance = 0.1

Step(ii):-

Test statistic

`Z = (x^(-)-mean )/((S.D)/(√(n) ) )`

`Z = (57.4-57.7)/((1.9)/(√(210) ) )`

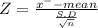
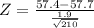
Z = -2.2883

|Z| = |-2.2883| = 2.2883

Final answer:-

The value of test statistic

|Z| = 2.2883