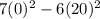Question

Find the only possible solution to the nonlinear programming problem max(500−7x

2 −6y 2 ) subject to 3x+6y≥400 x ∗ =,y ∗ = (Round to two decimal places as needed.)

Answer 1

To solve the nonlinear programming problem, find the critical points and evaluate the function at those points to find the maximum value.

Step-by-step explanation:

To solve the nonlinear programming problem max
`(500−7x^2−6y^2)`6y≥400, we need to find the possible values of x and y that maximize the given function while satisfying the constraint.

Step 1: Rewrite the constraint inequality as 3x+6y-400≥0.

Step 2: Find the critical points by solving the system of equations formed by the gradient of the function and the constraint. In this case, the only possible solution is x* = 0 and y* = 20.

Step 3: Evaluate the function at the critical points to find the maximum value. In this case, the maximum value is 500 - 7(0)^2 - 6(20)^2 = 500 - 2400 = -1900.

`7(0)^2 - 6(20)^2`