Question

Find the geometric power series for f(x)=5/(3x−1) centered at 1 , and find the interval of convergence.

Answer 1

The geometric power series for
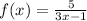`\( f(x) = (5)/(3x-1) \)` centered at x = 1 is
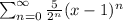`\( \sum_(n=0)^(\infty) (5)/(2^n)(x-1)^n \)`. The interval of convergence is
`\( |x-1| < (1)/(2) \)`.

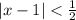Step-by-step explanation:

To find the geometric power series centered at \( x = 1 \), we use the formula for the geometric series:

`\[ f(x) = (a)/(1-r), \]`

where a is the first term and r is the common ratio. In our case, a = 5 and
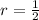`\( r = (1)/(2) \)`. Substituting these values, we get:

`\[ f(x) = (5)/(1-(1)/(2)) = (5)/((1)/(2)) = 10. \]`

Now, we express f(x) as a power series:

`\[ f(x) = \sum_(n=0)^(\infty) a_n(x-1)^n, \]`

where
`\( a_n \)` is the n-th term of the series. In our case,
`\( a_n = (5)/(2^n) \)`. Therefore, the geometric power series is:

`\[ \sum_(n=0)^(\infty) (5)/(2^n)(x-1)^n. \]`

For the interval of convergence, we use the ratio test. The ratio
`\( (a_(n+1))/(a_n) \) is \( (1)/(2) \),` which is independent of n. The series converges absolutely if |r| < 1 , so:

`\[ |x-1| < (1)/(2). \]`

Thus, the interval of convergence is
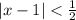`\( |x-1| < (1)/(2) \)`.