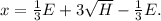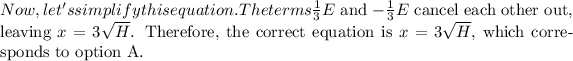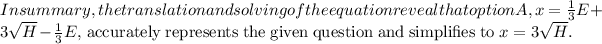Final Answer:
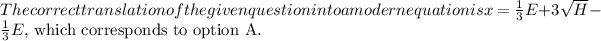
Step-by-step explanation:
Let's break down the translation of the question into an equation. The question states, "One-third of a herd of elephants and three times the square root of the remaining quantity." Let
 represent the herd of elephants, and
represent the herd of elephants, and
 represent the remaining quantity. The expression "One-third of a herd of elephants" is translated as
represent the remaining quantity. The expression "One-third of a herd of elephants" is translated as
 , and "three times the square root of the remaining quantity" is translated as
, and "three times the square root of the remaining quantity" is translated as
 . Combining these, we get the equation
. Combining these, we get the equation