Question

The matrix A=[ 8−6 k−8] has two distinct real eigenvalues if and only if k

Answer 1

The matrix A=[8 -6 k;-8 4 4;-4 2 3] has two distinct real eigenvalues if and only if the discriminant of its characteristic polynomial is positive. The discriminant can be found by solving an inequality.

Step-by-step explanation:

The matrix A=[8 -6 k;-8 4 4;-4 2 3] has two distinct real eigenvalues if and only if the discriminant of its characteristic polynomial is positive. The characteristic polynomial can be found by subtracting the identity matrix multiplied by a scalar, λ, from matrix A and taking its determinant:

`|8-λ -6 -k|-8 4 4|-4 2 3|=0`

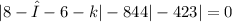
Expanding the determinant and simplifying will result in a quadratic equation in λ:

`λ^2 − 7λ + 12 − 107k = 0`

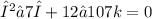
The discriminant of this quadratic equation is:

Δ = b^2 - 4ac = (-7)^2 - 4(1)(12-107k) = 49 + 4(107k - 12) = 428k - 19

For the matrix A to have two distinct real eigenvalues, the discriminant must be positive: 428k - 19 > 0

Solving this inequality results in:

k > 19/428