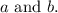Final answer:
The integers
 satisfy the equation
satisfy the equation
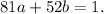
Step-by-step explanation:
To find integers ( a ) and ( b ) satisfying ( 81a + 52b = 1 ) using the Euclidean Algorithm, we initiate the process by expressing 81 and 52 as a linear combination in terms of each other. Beginning with the equation
 we rewrite it as ( 81 = 52 \times 1 + 29 \),
we rewrite it as ( 81 = 52 \times 1 + 29 \),
 . Proceeding iteratively, we express 52 as a linear combination of 29 and 81, repeating the process until we attain a form where the greatest common divisor of 81 and 52 equals 1.
. Proceeding iteratively, we express 52 as a linear combination of 29 and 81, repeating the process until we attain a form where the greatest common divisor of 81 and 52 equals 1.
Continuing the process, we eventually reach the equation
 is expressed as a linear combination of
is expressed as a linear combination of
 ( 52 \). Rearranging terms leads us to
( 52 \). Rearranging terms leads us to
 simplifying to
simplifying to
 . Consequently, by matching coefficients, we find that ( a = -9 ) and ( b = 14 ) satisfy the equation ( 81a + 52b = 1 ), demonstrating the solution derived through the Euclidean Algorithm.
. Consequently, by matching coefficients, we find that ( a = -9 ) and ( b = 14 ) satisfy the equation ( 81a + 52b = 1 ), demonstrating the solution derived through the Euclidean Algorithm.
This process showcases how the Euclidean Algorithm systematically computes the coefficients of the linear combination, ultimately solving for
 such that their combination results in the desired value. The obtained values satisfy the equation
such that their combination results in the desired value. The obtained values satisfy the equation
 , confirming the accuracy of the method used to determine the integers
, confirming the accuracy of the method used to determine the integers