Question

Quadratic Functions Wiggins, Roy Find all zeros of the function f(x)=x^(2)+3x-18 (-6,0),(3,0) (0,-6),(0,3) (-6,0),(0,3) (0,-6),(3,0)

Answer 1

A quadratic function is a second-order polynomial function that can be written in the form f(x) = ax^2 + bx + c. To find the zeros of a quadratic function, we use the quadratic formula. For the given function f(x) = x^2 + 3x - 18, the zeros can be found by substituting the values of a, b, and c into the quadratic formula and solving for x.

Step-by-step explanation:

A quadratic function is a second-order polynomial function of the form
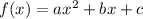`f(x) = ax^2 + bx + c`re constants. To find the zeros of a quadratic function, we set f(x) equal to zero and solve for x using the quadratic formula: x = (-b ± sqrt(b^2 - 4ac))/(2a).

For the given function f(x) = x^2 + 3x - 18, we substitute the values of a, b, and c into the quadratic formula to find the zeros.

Using the formula, we have: x = (-3 ± sqrt(3^2 - 4(1)(-18)))/(2(1)).

Calculating the values inside the square root, we get: x = (-3 ± sqrt(81 + 72))/(2).

Simplifying further, we have: x = (-3 ± sqrt(153))/(2).