Question

Use spherical coordinates to calculate the triple integral of f (x, y, z) over the given region.

x² +y² + z²≥ 1, x, y, z ≥ 0

Answer 1

To calculate the triple integral using spherical coordinates, express the function f(x, y, z) in terms of spherical coordinates. Set limits of integration for r, θ, and φ. Evaluate the triple integral to find the result.

Step-by-step explanation:

To calculate the triple integral using spherical coordinates, we need to express the function f(x, y, z) in terms of spherical coordinates. In spherical coordinates, the variables are r (the radial coordinate), θ (the polar angle), and φ (the azimuthal angle). The limits of integration for r are from 1 to infinity, for θ are from 0 to π/2, and for φ are from 0 to π/2. Then, we can set up the triple integral as:

`∫∫∫f(r, θ, φ) r^2 sin θ dr dθ dφ`

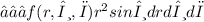
Finally, we can evaluate this triple integral to find the desired result.